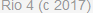Планетарные передачи АКП
Примечание: информация является универсальной и применима для всех типов АКПП независимо от производителя.
Содержание:
Устройство и принцип работы планетарного ряда
Расчёт передаточных чисел планетарного ряда
Планетарные механизмы с несколькими планетарными рядами
В гидромеханических автоматических коробках передач наибольшее распространение получили планетарные передачи. Планетарные передачи представляют собой наборы планетарных рядов, которые позволяют получить оптимальное передаточное число в соответствии с массой автомобиля, мощностными характеристиками двигателя и прочими параметрами конкретного автомобиля.
3.1. Устройство и принцип работы планетарного ряда
Планетарный ряд состоит из четырёх основных элементов:
1. Солнечной шестерни;
2. Коронной шестерни;
3. Сателлитов;
4. Водила.
Схема планетарного ряда показана на рис. 3.1.
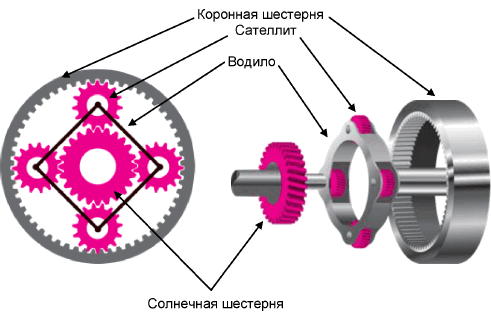
Рис. 3.1. Схема устройства планетарного ряда.
Своё название планетарная передача получила благодаря сходству движения сателлитов вокруг солнечной шестерни с движением планет вокруг солнца.
Сателлиты закреплены в корпусе водила, поэтому они могут вращаться вокруг своих осей, но не могут перемещаться относительно водила. Своими зубьями сателлиты входят в зацепление и с солнечной и с коронной шестернями, таким образом, солнечная шестерня зацепляется с коронной шестерней через сателлиты.
Для работы планетарного механизма необходимо чтобы один из элементов планетарного ряда был остановлен, тогда второй элемент планетарного ряда, соединённый с турбинным колесом гидротрансформатора будет ведущим, а оставшийся элемент планетарного ряда будет ведомым.
В таблице 3.1. приведены возможные комбинации остановленных, входных и выходных элементов при работе планетарного ряда.
Таблица 3.1. Возможные комбинации работы элементов планетарного ряда.
|
№ п/п |
Ведущий элемент |
Ведомый элемент |
Остановленный элемент |
Передаточное число планетарного ряда |
|
1 |
Солнечная шестерня |
Коронная шестерня |
Водило |
U > 1 |
|
2 |
Коронная шестерня |
Солнечная шестерня |
Водило |
U < 1 |
|
3 |
Солнечная шестерня |
Водило |
Коронная шестерня |
U > 1 |
|
4 |
Водило |
Солнечная шестерня |
Коронная шестерня |
U < 1 |
|
5 |
Коронная шестерня |
Водило |
Солнечная шестерня |
U > 1 |
|
6 |
Водило |
Коронная шестерня |
Солнечная шестерня |
U < 1 |
Передаточное число любой передачи определяется как отношение скоростей вращения ведущего и ведомого валов или соотношения крутящих моментов по следующей формуле:
U = n ведущего / n ведомого = М ведомого / М ведущего = Z ведомого / Z ведущего, (3.01)
где U - передаточное число передачи;
n ведущего - число оборотов ведущего элемента передачи, об/мин;
n ведомого - число оборотов ведомого элемента передачи, об/мин;
М ведомого - крутящий момент ведомого элемента передачи, Н-м;
М ведущего - крутящий момент ведущего элемента передачи, Н-м;
Z ведомого - число зубьев ведомого колеса,шт;
Z ведущего - число зубьев ведущего колеса, шт.
Общее передаточное число многоступенчатых передач вычисляется по формуле:
(3.02)
U = U1-U2-...-Un,
где U1, U2...Un - передаточные числа каждой ступени.
Если передаточное число больше 1, это означает, что скорость вращения ведомого элемента меньше, чем ведущего и передача увеличивает крутящий момент, подаваемый на ведущий элемент. И наоборот, если передаточное число меньше 1, это означает, что скорость вращения ведомого элемента больше, чем ведущего и передача уменьшает крутящий момент, подаваемый на ведущий элемент.
Согласно данных в таблице 3.1 один планетарный ряд позволяет получить шесть передач, причём три из них увеличивают скорость вращения ведомого элемента, а три уменьшают. Кроме того, когда остановлено водило планетарного ряда происходит изменение направление вращения ведомого элемента по отношению к ведущему, т.е. реализуется задняя передача.
Если ни один из элементов планетарного ряда не остановлен, то вне зависимости от ведущего и ведомого элементов, планетарный ряд не будет передавать крутящий момент, т.е. это будет нейтральная передача.
Если остановить любые два элемента планетарного ряда, то весь планетарный механизм будет неподвижным.
Соединение двух любых элементов планетарного ряда между собой приводит к блокировке планетарного ряда, соответственно, все элементы планетарного ряда вращаются с одинаковой скоростью, т.е. передаточное число U = 1 (прямая передача).
На основании перечисленных утверждений можно сделать вывод, что один планетарный ряд позволяет получить 8 передач - две передачи заднего хода, нейтральную передачу и пять передач переднего хода, включая прямую передачу.
1. Возможность получения большого количества передач(8 передач), а значит и широкий набор передаточных чисел.
2. Конструкция планетарного ряда имеет минимальное количество элементов, поэтому массовые и габаритные показатели имеют минимальные значения в сравнении с обычными цилиндрическими передачами.
3. В зацеплении постоянно участвуют сразу несколько сателлитов, поэтому планетарный ряд способен передавать большие крутящие моменты при минимальных габаритных размерах.
Основным недостатком планетарных передач является меньший КПД по сравнению с обычными цилиндрическими передачами. Это объясняется тем, что в зацеплении участвует большее количество зубьев, соответственно, потери на трение увеличены.
РАСЧЁТ ПЕРЕДАТОЧНЫХ ЧИСЕЛ ПЛАНЕТАРНОГО РЯДА
Расчёт планетарных передач существенно отличается от расчёта обычных цилиндрических передач, так как сателлиты совершают сразу два движения - вращение вокруг своих и осей и вращение вместе с водилом.
Существуют различные методы расчёта планетарных механизмов. Рассмотрим один из них, который называется расчётом методом обращения.
На рис. 3.2. представлена схема работы планетарного ряда, у которого ведущим элементом является солнечная шестерня, остановленным элементом является коронная шестерня, а ведомым элементом является водило.

Рис. 3.2. Схема работы планетарного механизма при остановленной коронной шестерне и ведущей солнечной шестерне.
Пусть солнечная шестерня вращается по часовой стрелке. Тогда сателлиты будут вращаться против часовой стрелки и отталкиваясь о неподвижные зубья коронной шестерни заставят водило вращаться по часовой стрелке. Получается, что сателлиты вращаются вокруг своих осей (совершают относительное движение) и одновременно вращаются вместе с водилом (совершают переносное движение).
Для лучшего понимания расчёта планетарных механизмов методом обращения зададим число зубьев каждого из элементов и запишем их в таблицу 3.2.
Таблица 3.2. Исходные данные для расчёта планетарного механизма.
|
Обозначение/ Элемент |
Солнечная шестерня |
Сателлиты |
Коронная шестерня |
|
Обозначение |
Z1 |
Z2 |
Z3 |
|
Число зубьев |
28 |
Не важно |
62 |
Для упрощения понимания работы планетарного механизма в расчётах используют кинематические схемы. На рис.3.3. приведена кинематическая схема работы планетарного механизма при остановленной коронной шестерне и ведущей солнечной шестерне. Здесь 1 -солнечная шестерня, 2 - сателлит, 3 - коронная шестерня и 4 - водило.
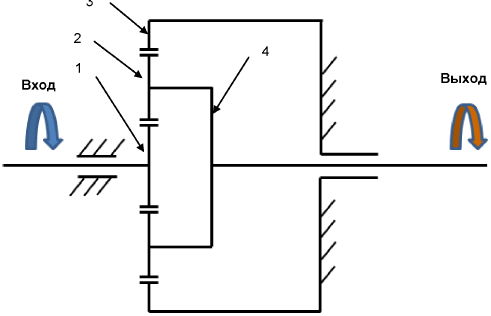

Рис. 3.3. Кинематическая схема планетарного механизма при остановленной коронной шестерне и ведущей солнечной шестерне.
При расчёте передаточного числа планетарного механизма используют следующие определения.
Исходный планетарный механизм - это планетарный механизм, передаточное число которого необходимо вычислить. Пусть исходным планетарным механизмом будет планетарный механизм, кинематическая схема которого представлена на рис. 3.3.
Передаточное число исходного планетарного ряда есть отношение числа оборотов входного вала к числу оборотов выходного вала (см. формулу 3.01):
Обращённый планетарный механизм - это планетарный механизм, ко всем элементам которого приложена угловая скорость водила, направленная в сторону, противоположную направлению вращения водила исходного планетарного механизма. Таким образом, водило планетарного ряда останавливается. Кинематическая схема обращённого планетарного механизма представлена на рис.3.4.

Рис.3.4. Кинематическая схема обращённого планетарного механизма.
Передаточное число обращённого планетарного механизма тоже определяется по формуле(3.01):
(3.04)
U обращ. = n1 обращ. / n3 обращ. ,
где U обращ - передаточное число обращённого планетарного механизма;
n1 обращ - скорость вращения входного элемента обращённого планетарного механизма, об / мин;
n3 обращ. - скорость вращения выходного элемента обращённого планетарного механизма, об / мин.
В обращённом планетарном механизме изображённом на рис.3.4. входным элементом является солнечная шестерня 1, остановленным элементом является водило 4, а выходным элементом является коронная шестерня 3.
Поскольку водило остановлено, то сателлиты 2 вращаются только вокруг своих осей.
Составим таблицу соответствия между исходным и обращённым планетарными механизмами.
Таблица 3.3. Таблица соответствия между исходным и обращённым планетарным механизмом (при остановленной коронной шестерне и ведущей солнечной шестерне исходного планетарного механизма).
|
планетарный механизм / обозначение элементов |
1 (солнечная шестерня) |
3 (коронная шестерня) |
4 (водило) | |
|
Исходный |
n1исх |
0 |
n4исх |
Скорость вращения |
|
Обращённый |
n1 обращ = n1 исх - n4 исх |
n3 обращ = - n4 исх |
0 |
Скорость вращения |
Скорость вращения выходного элемента обращённого планетарного механизма равна n3 обращ = - n4 исх (3.05).
Знак минус показывает, что направление вращения выходного элемента планетарного механизма противоположно направлению вращению входного элемента планетарного ряда.
Подставим в формулу (3.03) значения скоростей вращения соответствующих элементов из таблицы 3.3. Получим:
(3.06)
U обращ. = n1 обращ. / n3 обращ. = (n1исх - n4 исх) / - n4 исх
Упростим полученное выражение:
(3.07)
U обращ. = (n1 исх - n4 исх) / - n4 исх = 1 - n1 исх / n4 исх
Но согласно формулы (3.03) выражение n1исх / n4 исх есть передаточное число исходного планетарного механизма, поэтому окончательно получаем:
(3.08)
U обращ. = 1 - Uисх
Тогда,
(3.09)
Uисх = 1 - U обращ.
Вычислим передаточное число обращённого планетарного механизма используя данные таблицы 3.2. Поскольку в обращённом планетарном механизме все элементы совершают исключительно вращательное движение вокруг своих осей, можно применять формулы для расчёта обычных цилиндрических передач. Получим:
(3.10)
U обращ. = - (Z2 / Z1)-(Z3 / Z2) = - Z3 / Z1
Примечание. Знак минус показывает, что солнечная шестерня Z1 и сателлиты Z2 вращаются в разные стороны.
Окончательно получаем формулу для вычисления передаточного числа исходного планетарного механизма, подставляя формулу (3.10) в формулу (3.09):
(3.11)
Uсх = 1+ Z3 / Z1
Uсх = 1+ 62 / 28 = 3,214
Так как передаточное число исходного планетарного механизма больше единицы, то такой планетарный механизм увеличивает крутящий момент.
Рассмотренный метод расчета планетарных механизмов является универсальным для расчёта любых планетарных механизмов.
В качестве ещё одного примера вычислим передаточное число планетарного механизма, у которого входным элементом является водило, остановленным элементом является солнечная шестерня, а выходным элементом является коронная шестерня.
Кинематическая схема исходного планетарного механизма представлена на рис. 3.5.
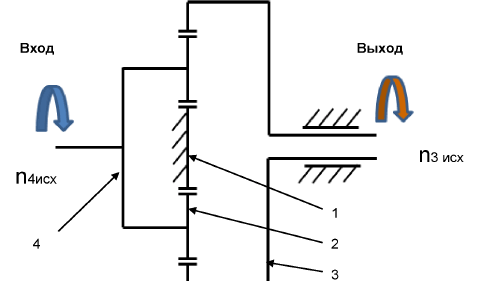
Рис. 3.5. Кинематическая схема исходного планетарного механизма при остановленной солнечной шестерне и ведущем водиле.
Передаточное число исходного планетарного ряда есть отношение числа оборотов входного вала к числу оборотов выходного вала (см. формулу 3.01):
Uисх = n вх / n вых = n4исх / nЗисх
(3.12)
Кинематическая схема обращённого планетарного механизма представлена на рис.3.6.
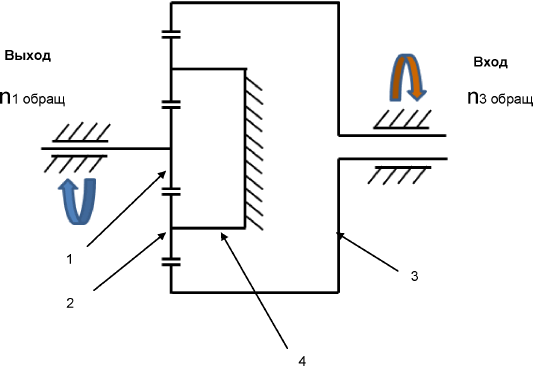
Рис.3.6. Кинематическая схема обращённого планетарного механизма.
Составим таблицу соответствия.
|
Планетарный механизм / обозначение элементов |
1 (солнечная шестерня) |
3 (коронная шестерня) |
4 (водило) | |
|
Исходный |
0 |
n3 исх |
n4исх |
Скорость вращения |
|
Обращённый |
n1обращ = - n4 исх |
n3 обращ = n3 исх - n4 исх |
0 |
Скорость вращения |
Расчёт планетарного механизма производим аналогично предыдущему варианту.
Передаточное число обращённого планетарного механизма определяется по формуле:
(3.13)
U обращ. = n3 обращ. / n1 обращ.
Скорость вращения входного элемента обращённого планетарного механизма равна
(3.14)
n3 обращ = n3 исх - n4 исх
Подставим в формулу (3.13) значения скоростей вращения соответствующих элементов из таблицы 3.4. Получим: (3.15)
U обращ. = n3 обращ. / n1 обращ. = (n3 исх - n4 исх) / - n4 исх
Упростим полученное выражение: (3.16)
U обращ. = (n3 исх - n4 исх) / - n4 исх = 1 - n3исх / n4 исх
Но согласно формулы (3.12) выражение n4 исх / n3 исх есть передаточное число исходного планетарного механизма, поэтому окончательно получаем: (3.17)
U обращ. = 1 - 1 / Uисх
Следовательно,
(3.18)
Uсх = 1 / (1 - U обращ.)
Вычислим передаточное число обращённого планетарного механизма используя данные таблицы 3.2. Поскольку в обращённом планетарном механизме все элементы совершают исключительно вращательное движение вокруг своих осей, можно применять формулы для расчёта обычных цилиндрических передач. Получим:
(3.19)
U обращ. = (Z2 / Z3)-( - Z1 / Z2) = - Z1 / Z3
Примечание. Знак минус показывает, что солнечная шестерня Z1 и сателлиты Z2 вращаются в разные стороны.
Окончательно получаем формулу для вычисления передаточного числа исходного планетарного механизма, подставляя формулу (3.19) в формулу (3.18):
(4.20)
Uисх = 1 / (1+ Z1 / Z3)
Uисх = 1 / (1+ 28 / 62) = 0,689
Так как передаточное число исходного планетарного механизма меньше единицы, то такой планетарный механизм увеличивает скорость вращения выходного элемента.
3.3. Планетарные механизмы с несколькими планетарными рядами
Как уже говорилось в разделе 3.1, один планетарный ряд позволяет получить пять передач переднего хода, две задних передачи и одну нейтральную передачу. Т.е. теоретически можно сконструировать 5-ти ступенчатую АКПП с одним планетарным механизмом. Однако практически такую схему не применяет ни один производитель АКПП. В АКПП любого производителя используется планетарный механизм, состоящий из нескольких планетарных рядов. Основные причины, по которым конструкторам приходится усложнять планетарную передачу, перечислены ниже.
1. Для упрощения конструкции АКПП, уменьшения габаритных размеров и массы выходной элемент планетарного механизма является единым для всех передач.
2. Если использовать один планетарный ряд, в котором выходной элемент будет единым для всех передач, то число передач планетарного ряда будет следующим:
- одна задняя передача;
- нейтральная передача;
- две передачи переднего хода, одна из которых будет иметь передаточное число U=1,0.
3. Если в АКПП только один планетарный ряд, нельзя использовать водило в качестве единого выходного элемента, так как в этом случае нельзя реализовать заднюю передачу.
Как видите, причин использования нескольких планетарных рядов в АКПП достаточно много. Существует много кинематических схем планетарных механизмов, которые позволяют получить необходимое количество передач. Самыми распространёнными кинематическими схемами являются схемы Симпсона и Равиньо.
Планетарная передача системы Симпсона состоит из двух планетарных рядов, у которых солнечные шестерни жёстко связаны друг с другом. Для управления работой планетарной передачи Симпсона использовались две муфты, два тормоза и одна одноходовая муфта. Такая кинематическая схема позволяла получить следующие передачи:
- нейтральную передачу;
- две понижающие передачи (первую и вторую);
- прямую передачу(U=1,0);
- заднюю передачу.
Кинематическая схема планетарной передачи Симпсона показана на рис.3.7.

Рис.3.7. Кинематическая схема планетарной передачи Симпсона.
С1, С2 - муфты;
В1, В2 - тормоза;
F - одноходовая муфта.
Общим выходным элементом планетарной передачи служит коронная шестерня правого (по рис. 3.7) планетарного механизма.
Недостатком такой кинематической схемы является отсутствие повышающей (четвёртой) передачи. Поэтому для получения повышающей передачи дополнительно устанавливался повышающий планетарный механизм. Такая кинематическая схема, состоящая из трёх планетарных рядов - повышающего ряда и планетарной передачи Симпсона, до сих пор применяется в АКПП AISIN 30-40LE, которые устанавливаются на автомобили HYUNDAI H-1(TQ).
Кинематическая схема АКПП AISIN 30-40LE показана на рис. 3.8. Применение дополнительного повышающего планетарного механизма повлекло за собой установку дополнительных муфт и тормозов, что существенно усложнило конструкцию АКПП.
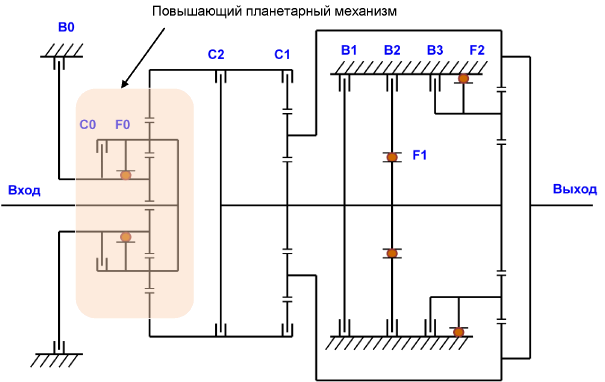
Рис. 3.8. Кинематическая схема 4-х ступенчатой АКПП AISIN 30-40LE с планетарной передачей Симпсона и повышающим планетарным механизмом.
С0, С1, С2 - муфты;
В0, В1, В2, В3 - тормоза;
F0, F1, F2 -одноходовые муфты.
Внешний вид АКПП серии AISIN 30-40LE показан на рис.3.9.

Рис.3.9. Внешний вид АКПП AISIN 30-40LE.
Планетарные передачи системы Равиньо (в английской транскрипции Ravigneaux) имеет абсолютно другую конструкцию. В этой планетарной передаче используется общее водило с тремя наборами сателлитов, общая коронная шестерня и две солнечных шестерни с разным количеством зубьев. Работой планетарного механизма управляют три муфты, два тормоза и одна одноходовая муфта. Планетарная передача Равиньо позволяет получить следующие передачи:
- нейтральную передачу;
- две понижающие передачи(первую и вторую);
- прямую передачу (U=1,0);
- повышающую передачу;
- заднюю передачу.
Планетарная передача Равиньо используется в АКПП серии A4AF3 и A4BF2, которые устанавливаются на автомобили HYUNDAI Getz, Elantra XD, Accent LC,MC.
Кинематическая схема планетарной передачи Равиньо показана на рис. 3.10.
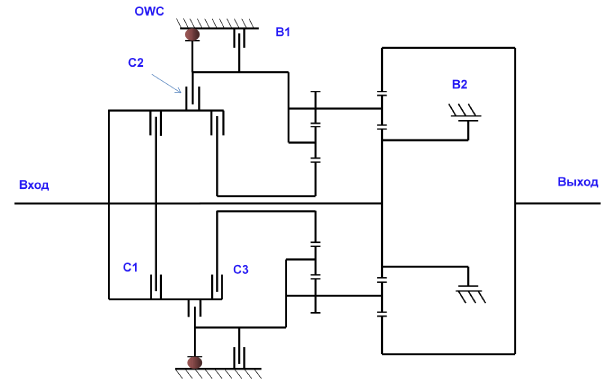
Рис. 3.10. Планетарная передача Равиньо АКПП A4AF3 и A4BF2 автомобилей HYUNDAI Getz, Elantra XD, Accent LC,MC.
В1, В2 - тормоза;
С1, С2, С3 - муфты;
OWC - одноходовая муфта.
АКПП серий F4A42, F4A51, A4CF имеют другую кинематическую схему, которая подробно рассмотрена в разделе 9.2.
На современной модельной линейке автомобилей HYUNDAI таких как Sonata YF, ix-35, Elantra MD применяются 6-ти ступенчатые АКПП серий A6LF, A6MF, A6GF. Это собственная разработка компании HYUNDAI. В планетарной передаче этих АКПП задействовано 3 планетарных механизма, три тормоза, две муфты и одна одноходовая муфта. Планетарная передача позволяет получить следующие передачи:
- нейтральную передачу;
- четыре понижающие передачи (с 1-ой по 4-ю передачи);
- прямую передачу (U=1,0)
- повышающую передачу;
- заднюю передачу.
Кинематическая схема АКПП серий A6LF, A6MF, A6GF показана на рис.3.10.
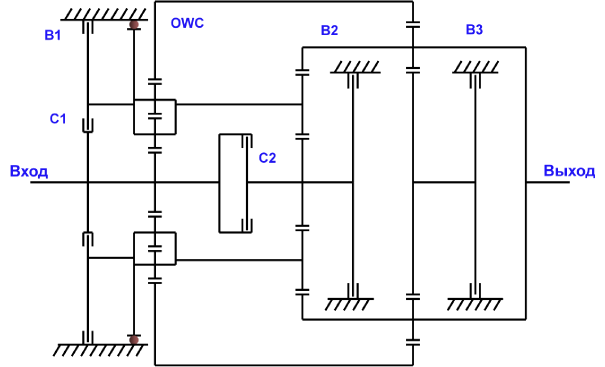
Рис. 3.10. Кинематическая схема АКПП серий A6LF, A6MF, A6GF.
В1, В2, В3 - тормоза;
С1, С2 - муфты;
OWC - одноходовая муфта.